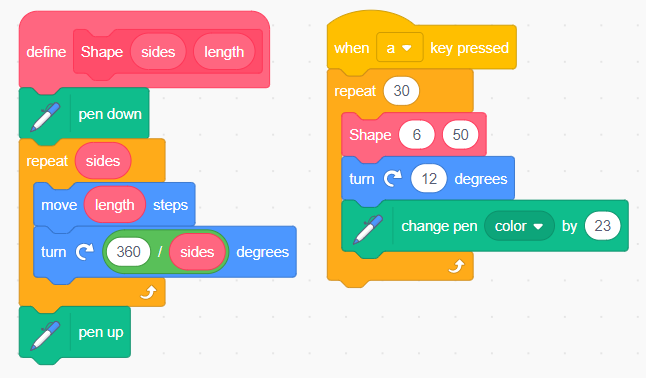
Shape – Looping Adaptable Procedures

Adaptable procedures extend ‘My Blocks’ by passing values to the procedures, which are used as variables. In the code here, the ‘Shape 4 60’ block calls the Shape procedure (set of instructions) passing two values to it. These are then used within the block to perform the instructions.

Looping these adaptable procedures means that you can call the procedure repeatedly. This allows for the construction of complex patterns with small amounts of code. However, manipulating them and controlling them to do what you want requires understanding.

You need to …

Know about variables
Understand the basic operation of the Pen extension of Scratch
Be taught about defining My Blocks using number variables
Be taught about the effect of nesting loops

This unit uses My Blocks with Loops to create shapes

Answer the following questions

Results

Self-Review

Look through the answers… Check to make sure you understand how each code works.

Run and Investigate the code in Scratch

Click Here

Modify the Code

Can you change the shapes drawn, or how many of them there are?

Make you own

Plan and make your own shapes using a procedure and a loop

Review

Look through the answers…

Check with an adult to make sure you understand how each code works.

Run and Investigate the code in Scratch

Click Here

Modify the Code

Can you change the shapes drawn, or how many of them there are?

Make you own

Plan and make your own shapes using a procedure and a loop

#1. Which sentence best describes what this code will do when the ‘a’ key is pressed?

It will rotate around, drawing 23 coloured 30-sided shapes.

It will rotate around, drawing 30 hexagons in different colours

It will rotate around, drawing 50 hexagons in 23 colours

It will rotate around, drawing six 50-sided shapes in lots of colours

When ‘a’ is pressed it will start the repeat 30

It will call the Shape procedure

to draw a 6-sided shape (hexagon) using sides 50 steps in length.

It then will turn 12 degrees clockwise

It will change the pen colour

It will draw 30 hexagons in total changing colour each time.

#2. What do you think it will look like?

It draws hexagons.

The colour changes for each hexagon

The turn angle is only 12 degrees meaning there will be 30 hexagons in 360 degrees

#3. Which command makes sure that the coloured hexagons are not all drawn on top of eachother?

Turn 12 degrees will mean that each hexagon is drawn facing in a different direction.

There will be some overlap or crossover, but none of them will be drawn in the same place.

#4. Using the Shape procedure, what outcome will this code draw when ‘b’ is pressed?

#5. Using the shape procedures, which statement best describes what this code will do?

It goes to (0,0), draws a shape, then moves further out and draws the shape again. It repeats this 12 times at different angles.

It goes to (0,0), draws a hexagon the moves further out and draws a triangle

It goes to (0,0), draws a six shapes and the moves further out and draws six more

Twelve times at different angles, It goes to (0,0), draws a hexagon, then moves further out and draws a triangle

#6. This code produce hexagons & triangles. Which do you think it will be?

#7. Which algorithm best describes this pattern

Repeat 8 times - turn 45, draw 1 pentagon, move out, draw a loop of 6 triangles, move out, draw a loop of 5 squares.

Start at (0,0), turn 45, draw 1 pentagon, move out, draw a loop of 5 triangles, move out, draw a loop of 6 squares.

Repeat 8 times - start at (0,0), turn 45, draw 1 pentagon, move out, draw a loop of 5 triangles, move out, draw a loop of 6 squares.

Repeat 8 times - start at (0,0), draw 8 pentagons, move out, draw a loop of 5 triangles, move out, draw a loop of 6 triangles..

#8. The green arrow points to part of the code. Which part of the shape does it draw?

Score and next steps

This page’s content is aligned to the Code-IT resources designed by Phil Bagge.
http://code-it.co.uk/goldshape/